Max Margin Planning for Continuous Domain
Let \({\mathcal {M}} \setminus R\) represent an MDP with an unknown reward function. The objective of IRL is to learn or estimate the reward function given demonstrations of behavior in the environment. In the early IRL work, the demonstrations are usually assumed to be provided by an expert. However in later work, this assumption is relaxed. The demonstrations come in the form of trajectories composed of state-action pairs \({\mathcal {T}}_m = \{(s_1,a_1),...,(s_{T_m},a_{T_m})\}\), where \(m=1,...,M\) represents the \(m^{th}\) expert trajectory, and \(T_m\) represents the number of time steps in the \(m^{th}\) trajectory. The set of all trajectories is denoted as \({\mathcal {T}}\).
Another assumption of IRL is that the expert is following an optimal policy with respect to their reward function \(R_E\) (this assumption also is relaxed in some of the more recent literature). An IRL algorithm attempts to recover the expert's reward function. The concept of IRL was first proposed by Russell (1998). He defines the IRL problem as determining the reward function optimized by an agent given 1) the agent's behavior over time and in varying circumstances, 2) measurements of the information given to the agent, and 3) a model of the environment. Russel does not propose an IRL algorithm but outlines several areas of future research for the field.
The IRL methods outlined in this section are divided into two categories. The first category is algorithms and represents the bulk of the IRL literature. The second category represents extensions of IRL. This category represents areas of research that go beyond the basic IRL paradigm and generally relax some of the assumptions of the problem formulation, e.g., multi-agent IRL. The former category is a well developed area of research while the latter represents areas that must be further developed in order for IRL to be widely applicable.
Algorithms
This section categorizes IRL methods based on the algorithm used to estimate the reward function (summarized in Table 1). The first category is max margin methods. The max-margin method was the first class of IRL algorithms and attempts to estimate rewards that maximize the margin between the optimal policy or value function and all other policies or value functions. IRL methods that match feature expectation are also categorized as max-margin methods because they share two traits. First, most of these methods assume that the reward is a linear combination of features and attempt to estimate the weights associated with the features. Second, feature expectation methods often maximize a slack variable in order to drive the estimated feature expectation to the empirical feature expectation.
The second category of IRL algorithms is Bayesian methods, which have two defining characteristics. The first is that the optimization routine maximizes the posterior distribution of the reward. The second is the use of prior distributions on the reward in order to define the posterior distribution. One advantage of Bayesian methods is the ability to convey prior information about the reward to the learning algorithm through the prior distribution. A second advantage is the ability for the Bayesian methods to account for complex behavior by modeling the reward probabilistically as a mixture of multiple reward functions.
The third category of IRL algorithms is maximum entropy methods. These methods are defined by using maximum entropy in the optimization routine to estimate the reward function. Maximum entropy methods are easily extended to the continuous space and can address sub-optimal expert demonstrations.
There are several IRL methods that do not fit nicely into these categories. Miscellaneous algorithms are outlined in the final subsection of this section. While there are some broad advantages to using a particular category of algorithm over another, as outlined, because of each method's nuance, intra-category differences must be considered, i.e., the strength of broad, category-wise comparisons beyond scholarly distinctions is limited. Instead, advantages and limitations of various methods are noted along the way, typically in following with historical development, in reference to IRL generally or other IRL methods in particular.
Maximum margin methods
The first paper published on IRL that presents methods for estimating the reward was written by Ng and Russell (2000) and outlines three max margin IRL algorithms. The first two assume that the expert's policy and the transition function are known. The third algorithm relaxes the assumption that the expert's policy is known but still requires a transition function. Ng and Russel propose that the reward function provides the most succinct description of an agent's behavior. More general methods, such as imitation learning or apprenticeship learning, attempt to learn the agent's policy from the set of demonstrations. However, the policy is dependent upon the system dynamics. If the dynamics change, the policy must change. By learning the reward function directly, an optimal policy for any transition function is learned.
The first IRL algorithm proposed by Ng and Russell (2000) makes three strong assumptions: 1) the policy is known, 2) the state transition dynamics are known, and 3) the state space is finite. Their primary result for this algorithm is the constraint
$$\begin{aligned} ({\varvec{P}}_{a_1} - {\varvec{P}}_a) ({\varvec{I}} - \gamma {\varvec{P}}_{a_1})^{-1} {\varvec{R}} \succeq 0, \end{aligned}$$
(5)
where \({\varvec{P}}_a\) is the transition matrix for action a, \(a_1\) is the action defined by the policy \(\pi (s) \equiv a_1\), and \({\varvec{R}}\) is a vector of rewards. This constraint defines all reward functions that are possible solutions to the IRL problem. However, the solution set contains \({\varvec{R}} = 0\) as well as numerous other solutions. To overcome this limitation, Ng and Russel propose a linear programming solution with a penalty term. This optimization problem is
$$\begin{aligned} \begin{aligned} \text {max}&\sum _{i=1}^I \underset{a \in \{a_2,...,a_K\}}{\text {min}}&\{ ({\varvec{P}}_{a_1}(i) - {\varvec{P}}_a(i)) ({\varvec{I}} - \gamma {\varvec{P}}_{a_1})^{-1} {\varvec{R}} \} - \lambda ||{\varvec{R}}||_1 \\&\text {s.t.}&({\varvec{P}}_{a_1} - {\varvec{P}}_a) ({\varvec{I}} - \gamma {\varvec{P}}_{a_1})^{-1} {\varvec{R}} \succeq 0 \quad \forall a \in {\mathcal {A}}\setminus a_1 \\&&|{\varvec{R}}_i| \le R_{\text {max}}, \quad i = 1...I, \end{aligned} \end{aligned}$$
(6)
where \({\varvec{P}}_a(i)\) denotes the \(i^{th}\) row of \({\varvec{P}}_a\), and \({\mathcal {A}}\setminus a_1\) represents all the actions in \({\mathcal {A}}\) except \(a_1\).
The second algorithm proposed by Ng and Russel assumes an infinite state space. A linear approximation is used for the reward function
$$\begin{aligned} R(s) = \alpha _1 \phi _1(s) + \alpha _2 \phi _2(s) + ... + \alpha _D \phi _D(s), \end{aligned}$$
(7)
where \(\phi _1,...,\phi _D\) are basis functions that are fixed and known. In this formulation, the weight parameters \(\alpha\) are assumed to be unknown and estimated by the IRL algorithm. The value function for a given policy can now be written as
$$\begin{aligned} V^\pi (s) = \alpha _1 V_1^\pi (s) + \alpha _2 V_2^\pi (s) + ... + \alpha _D V_D^\pi (s). \end{aligned}$$
(8)
For a policy to be optimal under the infinite state assumption, the following constraint must hold
$$\begin{aligned} {\mathbb {E}}_{s^\prime \sim P_{sa_1}}[V^\pi (s^\prime )] \ge {\mathbb {E}}_{s^\prime \sim P_{sa}}[V^\pi (s^\prime )] \quad \forall s,\; \text {and} \; \forall a \in {\mathcal {A}}\setminus a_1. \end{aligned}$$
(9)
The linear program for this algorithm is
$$\begin{aligned} \begin{aligned} \text {max} \sum _{s \in S_0}&\underset{a \in \{a_2,...,a_K\}}{\text {min}}&\{ p( {\mathbb {E}}_{s^\prime \sim P_{sa_1}}[V^\pi (s^\prime )] - {\mathbb {E}}_{s^\prime \sim P_{sa}}[V^\pi (s^\prime )]) \} \\&\text {s.t.}&|\alpha _d| \le 1, \quad d = 1,...,D, \\ \end{aligned} \end{aligned}$$
(10)
where \(S_0\) is a subsample of states in the infinite state space, and \(p(x) = x\) if \(x \ge 0\) and \(p(x) = 2x\) otherwise.
The third algorithm proposed by Ng and Russel addresses the more realistic case where the reward function is estimated from sample trajectories. Let \({\mathcal {D}}\) be a fixed initial state distribution. The objective of the IRL algorithm is to find the reward such that the unknown policy \(\pi\) maximizes \({\mathbb {E}}_{s_0 \sim {\mathcal {D}}}[V^\pi (s_0)]\). There are two assumptions for this algorithm. The first is that the optimal policy can be estimated. The second is the ability to simulate trajectories from the MDP. The second assumption allows for the transition function to be estimated from the sampled trajectories and does not need to be known a priori. The sampled trajectories are used to estimate \({\hat{V}}_d^\pi (s_0)\) for \(d=1,...,D\). Given a set of policies \(\{ \pi _1,...,\pi _I \}\), the optimization problem becomes
$$\begin{aligned} \begin{aligned} \text {maximize}&\sum _{i=1}^I p \left( {\hat{V}}^{\pi ^*}(s_0) - {\hat{V}}^{\pi _i}(s_0) \right) \\ \text {s.t.}&|\alpha _d| \le 1, \quad d = 1,...,D. \\ \end{aligned} \end{aligned}$$
(11)
This optimization problem returns a new set of \(\alpha\)'s and thus a new reward R. A new optimal policy is found using R, and the new policy is added to the set of policies. The algorithm is then repeated for a set number of iterations or until some measure of convergence is met.
Abbeel and Ng (2004) develop an IRL algorithm for apprenticeship learning that finds a policy that mimics that of the expert's by first estimating the reward function and then finding an optimal policy for the estimated reward function. The proposed IRL algorithm assumes that the reward can be expressed as a linear combination of known features and that the objective of the algorithm is to find the weights corresponding to each feature. Given this assumption, the value of a policy can be written as \({\mathbb {E}}_{s_0 \sim {\mathcal {D}}}[V^\pi (s_0)] = \alpha \mu (\pi )\). The apprenticeship learning algorithm attempts to find a policy \({\widetilde{\pi }}\) that minimizes \(||\mu ({\widetilde{\pi }}) - \mu _E||\), where \(\mu _E\) is the feature expectation of the expert. The expert's feature expectation can be estimated from the supplied trajectories. This optimization problem is written as
$$\begin{aligned} \begin{aligned} \text {max}_{\alpha ,t}&\quad t \\ \text {s.t.}&\quad \alpha ^\intercal \mu _E \ge \alpha ^\intercal \mu ^{(j)} + t, \quad j = 0,...,i-1 \\&\quad ||\alpha ||_2 \le 1, \\ \end{aligned} \end{aligned}$$
(12)
where \(\mu ^{(j)}\) represents the feature expectation under the \(j^{th}\) candidate policy. Abbeel and Ng also provide a simpler algorithm which they call the projection method. In a following study, Abbeel et al. (2008) adapt the max margin formulation to a path planning setting.
Syed and Schapire (2008) point out that a drawback to the method proposed by Abbeel and Ng (2004), and a limitation of many IRL algorithms, is that the performance of the agent learning the policy is limited to the quality of the expert. If the expert is not optimal, the learned policy will also be sub-optimal. In response, Syed and Schapire propose a game-theoretic approach to apprenticeship learning and IRL called multiplicative weights for apprenticeship learning (MWAL). The apprenticeship learning problem is posed as a two-player zero sum game. The goal of the learning agent (apprentice) is to maximize performance with respect to the expert even if the expert is playing sub-optimally. A key aspect of MWAL is the ability to impart prior knowledge to the learning agent about the importance of features. Syed, Bowling, and Schapire later use a linear programming approach to modify the MWAL algorithm so that it outputs a stationary policy (Syed et al. 2008).
As pointed out by Syed and Schapire, the reliance on expert demonstrations is a significant limitation in early IRL research. Following Syed and Schapire, several studies have addressed this limitation. Valko et al. (2013) extend the max margin formulation to the semi-supervised case where trajectories provided by an expert are assumed to be the labeled examples and trajectories provided by a non-expert are assumed to be the unlabeled examples. Zhou and Li (2018) develop a safety-aware version of max margin apprenticeship learning. A policy learned through apprenticeship learning can lead an agent into an unsafe state because an expert only supplies positive examples. Formal verification is incorporated into the learning process. If an estimated policy violates a safety specification, a negative example is generated. The negative examples are incorporated into the objective function, and a safety-aware policy is generated.
Another limitation of the algorithm proposed by Abbeel and Ng (2004) is sensitivity to the scaling of the features. In response, Neu and Szepesvári (2007) use gradient optimization techniques and IRL concepts to tackle the apprenticeship learning problem. They formulate the following objective function
$$\begin{aligned} J(\alpha ) = \sum _{s \in {\mathcal {S}}, a \in {\mathcal {A}}} \mu _E(s) ( \pi (a|s) - \pi _E(a|s))^2, \end{aligned}$$
(13)
and minimize \(J(\alpha )\) using the gradient
$$\begin{aligned} \frac{\partial \pi _\alpha }{\partial \alpha _k} = \pi _\alpha (a|s) \beta \left( \frac{Q_\alpha ^*(s,a)}{\partial \alpha _k} - \sum _{a' \in {\mathcal {A}}} \pi _\alpha (a'|s) \frac{Q_\alpha ^*(s,a')}{\partial \alpha _k} \right) . \end{aligned}$$
(14)
Ratliff et al. (2006) propose maximum margin planning where the objective is to find a linear mapping of features to rewards so that the policy estimated from the reward function is "close" to the behavior in the demonstrations. They outline a quadratic program that incorporates a slack variable \(\zeta\) that allows for violations of the constraint similar to the solution to support vector machines. The quadratic program is
$$\begin{aligned} \begin{aligned}&\text {min}_{\alpha ,\zeta _m}&\frac{1}{2} ||\alpha ||^2 + \frac{\gamma }{M} \sum _{m=1}^M \beta _m \zeta _m \\&\text {s.t.}&\alpha ^\intercal f_m(y_m) + \zeta _m \ge \text {max}_{y \in {\mathcal {Y}}_m} \alpha ^\intercal f_m(y) + {\mathcal {L}}_m(y), \quad \forall m, \end{aligned} \end{aligned}$$
(15)
where y is the desired trajectory, \(f(\cdot )\) is the expected feature count, \({\mathcal {L}}(\cdot )\) is the loss function, and \(\gamma\) and \(\beta\) are hyperparameters. If both the expected feature count and loss function are linear in the state-action space, the quadratic program can be transformed into a compact quadratic program. Ratliff et al. outline an efficient optimization algorithm and provide an algorithm for an online setting. The concept of maximum margin planning is later extended and generalized (Ratliff et al. 2006, 2009). Zou et al. (2018) build upon maximum margin planning and utilize deep learning to model human driving behavior in two capacities. The first is to extract relevant feature information from raw sensor input to represent the state information. The second is to estimate a policy given the current estimate of the reward function.
One of the limitations of max margin planning, and other IRL methods that rely on feature expectation, is that they require enough data (expert trajectories) to adequately estimate the expectation. Boularias and Chaib-Draa (2013) propose two bootstrapping methods that can improve the calculation of the feature expectation when only a small number of trajectories are provided by the expert. They demonstrate these methods on max margin planning and linear programming apprenticeship learning.
Most IRL algorithms assume that the state information is readily available to the algorithm. However, in many real-world applications, state information is only partially observable. For example, the state of the system may not be directly observable but a noisy sensor measurement that conveys some information about the state is available. In these instances, a partially observable MDP (POMDP) is used to model the sequential decision making process. Choi and Kim (2011) extend the algorithms presented by Ng and Russell (2000) and Abbeel and Ng (2004) to the partially observable case. Later, Chinaei and Chaib-Draa (2012) further extended the concept of IRL using POMDPs and demonstrate their proposed algorithm on a healthcare dialogue system.
Bayesian IRL
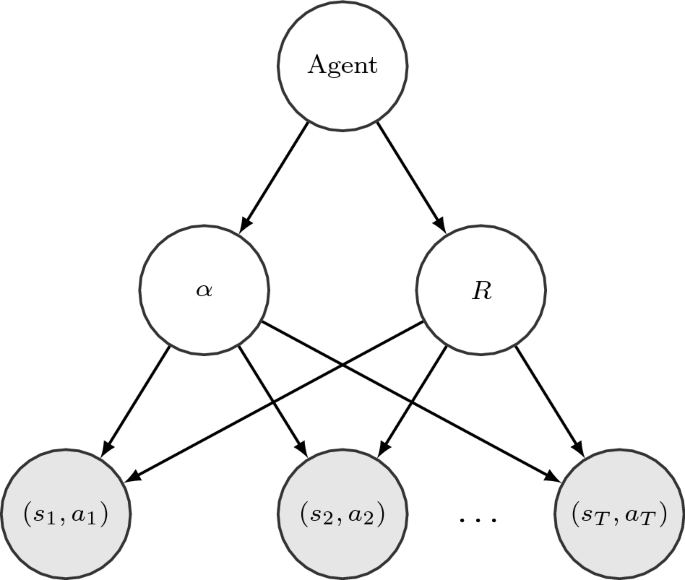
The Bayesian IRL model from Ramachandran and Amir (2007)
In general, Bayesian methods combine prior knowledge with data or evidence. Bayesian IRL techniques consider the expert's actions as the evidence used to update the estimate of the reward function. The first Bayesian IRL method uses a modified Markov Chain Monte Carlo (MCMC) algorithm to infer the reward function (Ramachandran and Amir 2007). The model for this Bayesian IRL formulation is diplayed in Fig. 2. Ramachandran and Amir state several advantages to their proposed Bayesian IRL algorithm. First, an optimal policy is not required. Second, it is not assumed that the expert has infallible decision making. Third, as in Bayesian IRL generally, external information about the problem can be incorporated into the reward function through the prior distribution. The probability of each state-action pair is assumed to be independent so the likelihood can be written as
$$\begin{aligned} {\mathbb {P}}({\mathcal {T}}|R) = {\mathbb {P}}((s_1, a_1)|R) {\mathbb {P}}((s_2, a_2)|R)...{\mathbb {P}}((s_T, a_T)|R). \end{aligned}$$
(16)
The likelihood of each state-action pair is modeled using an exponential distribution and a Q function conditioned on R
$$\begin{aligned} {\mathbb {P}}((s_t, a_t)|R) = \frac{1}{Z_t} e^{\alpha Q_R^*(s_t,a_t)}, \end{aligned}$$
(17)
where \(\alpha\) is a parameter that represents the confidence, and \(Z_t\) is the normalizing constant. The likelihood of the entire trajectory is written as
$$\begin{aligned} {\mathbb {P}}({\mathcal {T}}|R) = \frac{1}{Z} e^{\alpha E_R({\mathcal {T}})}, \end{aligned}$$
(18)
where \(E_R({\mathcal {T}}) = \sum _{t=1}^T Q_R^*(s_t,a_t)\). Using Bayes theorem, the posterior for R can now be rewritten as
$$\begin{aligned} {\mathbb {P}}(R|{\mathcal {T}}) = \frac{1}{Z'} e^{\alpha E_R({\mathcal {T}})} {\mathbb {P}}(R). \end{aligned}$$
(19)
The normalizing constant \(Z'\) can be difficult to calculate. The proposed sampling algorithm Policy Walk uses the ratio of posterior probabilities so \(Z'\) does not need to be calculated. Rothkopf and Ballard (2013) extend this Bayesian formulation and the Policy Walk algorithm to modular MDPs (see (Rothkopf and Ballard 2010) for more information on modular MDPs).
The original Bayesian IRL formulation is limited because it cannot easily estimate reward structures for states that are not visited by the expert. Michini and How (2012) propose an extension to the Bayesian IRL method in Ramachandran and Amir (2007) by using a kernel function to estimate the similarity between states. When new candidate rewards are selected at random, more weight is given to states that are similar to those visited by the expert. This Bayesian method improves time to convergence and allows the user to tradeoff computation time for solution accuracy. Gaussian process IRL (Levine et al. 2011) is an extension of Bayesian IRL that also uses a kernel function to help estimate the reward for unvisited or unseen states.
Choi and Kim (2011) propose a Bayesian IRL framework that finds the maximum-a-posteriori (MAP) reward using a gradient method. They select the MAP estimate for the reward over the mean posterior reward commonly used in Bayesian IRL methods because the mean posterior reward can produce a policy inconsistent with the observed expert's behavior. This property is due to integrating over the entire reward space. Conversely, the MAP reward is simply a point that maximizes the posterior and is thus robust to rewards in the tail of the distribution.
The MAP solution to the IRL problem is \(R_{MAP} = \text {argmax}_R [\log {\mathbb {P}}({\mathcal {T}}|R) + \log {\mathbb {P}}(R)]\). It is generally assumed that the likelihood is a differentiable function of the experts' trajectories and either \(V^*\) or \(Q^*\). Choi and Kim provide theorems that demonstrate that \(V^*\) and \(Q^*\) are convex and differentiable almost everywhere. If the prior on the reward is selected so that it is also differentiable, gradient descent can be used to find the MAP estimate \(R_{new} = R + \delta \nabla _R {\mathbb {P}}(R|{\mathcal {T}})\), where \(\delta\) is the step size.
Qiao and Beling (2011) provide MAP estimates for the reward function by formulating it as a quadratic convex programming problem. The reward is written as the vector \(\mathbf{r} \in {\mathbb {R}}^n\) and Gaussian priors are assigned to \(\mathbf{r} \sim {\mathcal {N}}(\mathbf{r} |\varvec{\mu }, \Sigma )\). The posterior distribution is derived using Bayes rule
$$\begin{aligned} {\mathbb {P}}(\mathbf{r} |{\mathcal {T}}) = \frac{1}{(2\pi )^{n/2} |\Sigma |^{1/2}} \exp \left( -\frac{1}{2} (\mathbf{r} - \varvec{\mu })^\intercal \Sigma ^{-1} (\mathbf{r} - \varvec{\mu }) \right) . \end{aligned}$$
(20)
Using the constraint proposed by Ng and Russell (2000), the IRL problem is written as the following quadratic program
$$\begin{aligned} \begin{aligned}&\text {min}_\mathbf{r}&\frac{1}{2} \left( (\mathbf{r} - \varvec{\mu })^\intercal \Sigma ^{-1} (\mathbf{r} - \varvec{\mu }) \right) , \\&\text {s.t.}&({\varvec{P}}_{a^*}-{\varvec{P}}_a)({\varvec{I}}_n-\gamma {\varvec{P}}_{a^*})^{-1}{} \mathbf{r} \ge 0 \quad \forall a \in {\mathcal {A}}, \\&&\mathbf{r} _{min} \le \mathbf{r} \le \mathbf{r} _{max}. \end{aligned} \end{aligned}$$
(21)
Qiao and Beling also use a preference graph and Gaussian processes to deal with problems in large or infinite state spaces. In a later work, Qiao and Beling (2013) use their Gaussian process method to recognize different agents based on their sequence of actions.
In many IRL implementations, expert trajectories are collected from multiple agents and it is assumed that all agents are maximizing the same reward function. Choi and Kim (2012) propose a nonparametric Bayesian formulation that does not assume that a single expert is maximizing a single reward function. A Dirichlet process mixture model is utilized to relax this assumption and estimate multiple rewards. Trajectories are assigned to clusters where each cluster is assumed to have a different reward structure. Under this formulation, an expert's behavior is generated from the following process:
- 1.
Draw a cluster assignment using the Dirichlet process.
- 2.
Draw the reward from the prior \(\prod _{d=1}^D {\mathcal {N}}(r_{k,d}|\mu ,\sigma )\) where k represents the cluster assignment, and d is the component of the reward function.
- 3.
Draw the trajectory from the likelihood function given the cluster-specific reward and \(\alpha\).
A Metropilis-Hasting algorithm (Chib and Greenberg 1995) is utilized for inference. Figure 3 displays the graphical model for this IRL method. Later, Choi and Kim (2013) propose an extension that can learn composite features called Bayesian non-parametric feature construction IRL (BNP-FIRL). Budhraja and Oates (2017) build upon the BNP-FIRL framework and utilize neural networks and neuroevolution to map state features to estimates of state values. Neuroevolution of augmenting topologies (NEAT) (Stanley and Miikkulainen 2002) utilizes a genetic algorithm to find the optimal number of layers and nodes for a neural network. Budhraja and Oates combine IRL and NEAT.
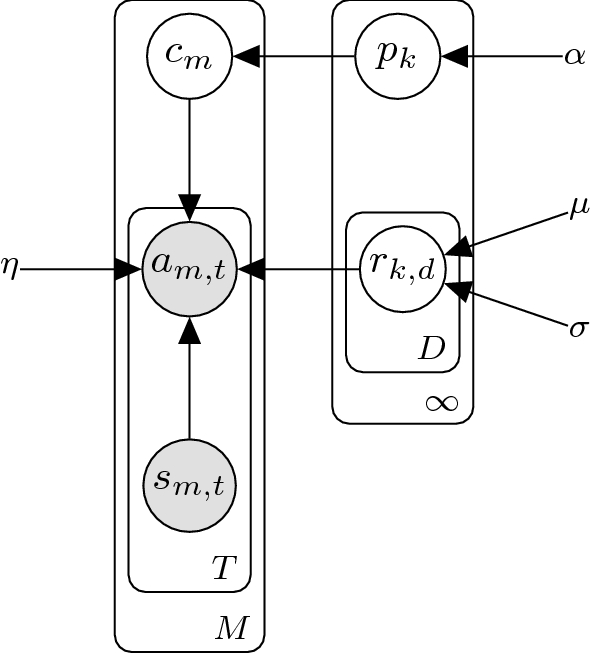
Graphical model non-parametric Bayesian IRL formulation from Choi and Kim (2012)
Michini and How (2012) approach the single reward function assumption in a similar fashion by using a Chinese restaurant process (CRP) prior (Griffiths et al. 2004) to partition the reward into subgoals. The CRP is similar to the Dirichlet process used by Choi and Kim (2012), but is more flexible. The CRP can allow for data-dependent selection of parameters and functional dependence on the current partition. The primary advantage of the proposed Bayesian nonparametric IRL (BNIRL) method is that the partitioned rewards can be very simple and thus easier to learn. Complex reward functions can be expressed as multiple simple subgoals.
The BNIRL method does not scale well to large state spaces because it requires calculating the optimal value function in order to evaluate the proposed reward. Michini et al. (2013) propose two solutions that do not require solving the full MDP. The first uses real-time dynamic programming, and the second modifies BNIRL to use a closed-loop controller instead of solving the MDP. Later, Michini et al. (2015) combine their work in Michini and How (2012) and Michini et al. (2013) and extend it to the continuous space using Gaussian processes.
Šošic et al. (2018) outline a significant limitation to the BNIRL method proposed by Michini and How. The BNIRL method is restricted to pure subgoal extraction and does not provide a mechanism to forecast expert behavior. This is due to the exchangeability in subgoal assignment in the original formulation. Thus, the recovered subgoals do not exhibit behavior similar to the expert's behavior. To address this limitation, Šošic et al. propose distance-dependent Bayesian nonparametric IRL (ddBNIRL) which replaces the exchangeable prior with a non-exchangeable prior and allows for information from visited states to be conveyed to non-visited states through a distance metric. This IRL formulation is later extended to address spatio-temporal relationships and time invariance (Šošić et al. 2018).
Lee et al. (2016) propose using a leveraged Gaussian process to incorporate negative examples into the reward learning process. One of the main limitations of IRL is the concentration of demonstrations around high reward states. The proposed method models a demonstrator that provides both positive and negative demonstrations characterized by a continuous proficiency parameter between − 1 and 1. A proficiency of 1 represents a positive example, or what the agent should do, and a proficiency of − 1 represents a negative example, or what the agent should not do.
Most IRL algorithms assume that the agents providing the sample trajectories are trustworthy, i.e., they are attempting to maximize the reward function. Zheng et al. (2014) propose robust Bayesian IRL to address the issue of sparse noise in the examples. Sparse noise describes the case where a majority of the demonstrations are trustworthy but a small number are untrustworthy. They motivate their work with a cab driver example. Most cab drivers are optimizing a single reward function. However, new cab drivers may not yet be experts and not follow the optimal route. Dishonest cab drivers may intentionally select a longer route to increase fairs. Robust Bayesian IRL includes a parameter that estimates the reliability of the demonstrations and uses the expectation-maximization (EM) algorithm (Dempster et al. 1977) to estimate the parameters.
Rothkopf and Dimitrakakis (2011) pose IRL as a preference elicitation problem where the goal is to infer if the decision maker prefers one set of events over another. For this formulation, it is assumed that there is some ordering to events and that each event has a utility where the decision maker is trying to maximize expected utility. Using these assumptions, the objective in the IRL problem is to assign numerical values to the utility. Rothkopf and Dimitrakakis define a structured prior on both the reward and the policy and then derive two Markov chain procedures for inferring the reward. Dimitrakakis and Rothkopf (2011) later expand this formulation to the multitask setting through the selection of priors on the reward and policy.
Hidden MDPs (hMDPs) (Kitani et al. 2012) were developed for the situation where the observer receives noisy state information. hMDPs are similar to partially observable MDPs but in hMDPs the state is known to the agent interacting with the environment and it is the observer collecting the trajectories that receives noisy state information. Surana (2014) proposes a Bayesian framework for the IRL problem for hMDPs where the observer is provided noisy observations \(y_{1:T} = \{y_1,...,y_T\}\) in place of the true state sequence. Surana notes that given \(\pi\), a hMDP reduces to a hidden Markov model (Rabiner 1989). MCMC methods can be used to sample the posterior for both the hidden states and the reward.
Brown and Niekum (2018) use the Bayesian IRL formulation to determine bounds on the performance of a policy. In this method, MCMC sampling is used to draw samples of an expert's reward function from the posterior distribution estimated using IRL, which is assumed to be an optimal policy. The loss is calculated between the evaluation policy and the policy estimated by IRL. A worst-case bound for the evaluation policy is also derived.
Maximum entropy IRL
Ziebart et al. (2008) propose the first maximum entropy IRL technique and claim that the proposed method addresses both noise in the trajectory and imperfect behavior. In the proposed maximum entropy IRL method, it is assumed that a learner is observing an agent, and that the agent is maximizing a function that linearly maps the state features to rewards. Ziebart et al. utilize the same concept as Ng and Russell (2000) and attempt to match expected feature counts with observed feature counts from the expert's trajectories. However, Ziebart et al. take a probabilistic perspective and model the probability of observing any single trajectory as
$$\begin{aligned} {\mathbb {P}}({\mathcal {T}}_m | \theta ) = \frac{1}{Z(\theta )} e^{\theta ^\intercal \mathbf{f} _{{\mathcal {T}}_m}}, \end{aligned}$$
(22)
where \(\theta\) is a vector of feature weights, \(\mathbf{f} _{{\mathcal {T}}_m} = \sum _{s_j \in {\mathcal {T}}_m} \mathbf{f} _{s_j}\) is the path feature count, and \(Z(\theta )\) is the partition function given the feature weights. Equation 22 models the trajectory for deterministic behavior. For non-deterministic behavior, the transition probability is included and the probability of observing a set of trajectories is
$$\begin{aligned} {\mathbb {P}}({\mathcal {T}} | \theta , P) \approx \frac{e^{\theta ^\intercal \mathbf{f} _{{\mathcal {T}}}}}{Z(\theta , P)} \prod _{s_{t+1}, a_t, s_t} P_{s_t, s_{t+1}}^{a_t}. \end{aligned}$$
(23)
The reward weights are learned from the demonstrated behavior by maximizing the log likelihood \(L(\theta )\) under the entropy distribution (Eq. 23)
$$\theta ^{*} = \arg \max_{\theta } \sum\limits_{{m = 1}}^{M} {\log } {\mathbb{P}}({\tilde{\mathcal{T}}}_{m} |\theta ,P),$$
(24)
where \({\tilde{\mathcal{T}}}_{m}\) is the \(m^{th}\) observed trajectory. Gradient descent is used to maximize the likelihood and the gradient is
$$\begin{aligned} \begin{aligned} \nabla L(\theta )&= \tilde{\mathbf{f }} - \sum _{\mathcal {T}} {\mathbb {P}}({\mathcal {T}}| \theta , P) \mathbf{f} _{\mathcal {T}} \\&= \tilde{\mathbf{f }} - \sum _{s_i} D_{s_i} \mathbf{f} _{s_i}, \end{aligned} \end{aligned}$$
(25)
where \(\tilde{\mathbf{f }}\) is the empirical feature count, and \(D_{s_i}\) is the expected state visitation frequency, which Ziebart et al. provide an efficient algorithm to calculate.
Later works characterize maximum entropy IRL as IOC and utilize it for human behavior modeling (Ziebart et al. 2009) and pointing target prediction (Ziebart et al. 2012). Other works expand into the continuous space using the maximum entropy concept (Aghasadeghi and Bretl 2011; Kalakrishnan et al. 2013, 2010; Levine and Koltun 2012). Furthermore, Ziebart et al. (2013) propose the concept of maximum casual entropy for interacting processes and demonstrate how this concept can be applied to the IOC problem. Bloem and Bambos (2014) and later Zhou et al. (2018) extend maximum casual entropy to the infinite time horizon problem.
One of the major limitations of IRL is the reliance on successful demonstrations provided by the expert. To address this limitation, Shiarlis et al. (2016) modify the maximum casual entropy formulation to incorporate unsuccessful demonstrations. A constraint is added to the optimization problem that forces the algorithm to find reward weights that not only minimize the difference between the empirical feature expectation for the successful examples and the learned feature expectation, but also maximize the difference between the empirical feature expectation for the unsuccessful examples and the learned feature expectation.
Another approach to overcoming the limitation of the demonstrations being provided solely by an expert combines maximum entropy IRL with semi-supervised learning (Audiffren et al. 2015). In this formulation, the supervised examples \(\Sigma ^* = \{{\mathcal {T}}_i^*\}_{i=1}^l\) are those provided by the expert, and the unsupervised examples \({\tilde{\Sigma }} = \{\tilde{{\mathcal {T}}}_j\}_{j=1}^u\) are those provided by a non-expert. It is assumed that the function \(s({\mathcal {T}},{\mathcal {T}}')\) is provided and measures the similarity between two trajectories. A pairwise penalty is defined
$$\begin{aligned} \Psi (\theta | \Sigma ) = \frac{1}{2(l+u)} \sum _{{\mathcal {T}}, {\mathcal {T}}' \in \Sigma } s({\mathcal {T}},{\mathcal {T}}') (\theta (\mathbf{f} _{\mathcal {T}}-\mathbf{f} _{{\mathcal {T}}'}))^2, \end{aligned}$$
(26)
where \(\Sigma = \Sigma ^* \cup {\tilde{\Sigma }}\). This penalty term is added to Eq. 24 to estimate the reward weights
$$\begin{aligned} \theta ^* = \text {argmax}_\theta (L(\theta |\Sigma ^*) - \lambda \Psi (\theta |\Sigma )), \end{aligned}$$
(27)
where \(\lambda\) is the tradeoff parameter between the log likelihood and the similarity between the supervised and unsupervised trajectories. There are numerous possible choices for the similarity function, but while a handcrafted function would perform the best, a radial basis function is a suitable selection.
Bogert et al. (2016) adapt maximum entropy IRL to partially observed trajectories. In this context, both states and actions can be occluded. Bogert et al. propose using the EM algorithm (Dempster et al. 1977) to estimate the missing information in the provided trajectory. However, computing the expectation becomes intractable as the size of the trajectory grows or multiple trajectories are provided by multiple experts. Therefore, Bogert and Doshi (2017) propose modeling the process generating the trajectories as a dynamic Bayesian network and demonstrate that Gibbs sampling can be used to perform fast inference on the latent variables.
Byravan et al. (2015) address scaling issues with maximum entropy IRL and continuous state spaces by discretizing the continuous trajectories into a graph. Once a sufficiently coarse graph is created, maximum entropy IRL is used to estimate the reward function. Shimosaka et al. (2017) build on this graph-based concept and adapt the creation of the graph to situations where the state space contains temporal information and transitions can vary depending on this information.
Wulfmeier et al. (2016) use deep architectures to map sensory information to reward function parameters in a path planning problem. This type of application, especially in a dense urban environment, requires a complex non-linear reward function. A maximum entropy deep IRL algorithm is proposed that can scale to large complex environments but requires a large number of expert trajectories. For the demonstration on urban driving, the inputs into the neural network are visual sensors (including 2D and 3D LIDARs), and over 25,000 trajectories where used as expert demonstrations. Wulfmeier et al. (2017) later expand on this initial study and include more indepth discussion and experimentation. Chen et al. (2019) and Finn et al. (2016) extend maximum entropy deep IRL to continuous action and state spaces.
Mendez et al. (2018) propose efficient lifelong IRL where the maximum entropy formulation is extended to an agent continually learning multiple tasks. It is assumed that an expert can provide demonstrations to the agent for each task. The agent sequentially learns the parameters of the reward function for a task before moving on to the next task. In order to improve efficiency, a transfer learning framework is proposed so that the agent can learn parts of the reward function from previously learned similar tasks. Yu et al. (2019) develop probabilistic embeddings for meta-inverse reinforcement learning (PEMIRL), which combines aspects of maximum entropy IRL, meta-learning, and deep generative models to learn reward functions that can generalize to new tasks with only a single demonstration provided by the expert. Ranchod et al. (2015) propose non-parametric Bayesian reward segmentation (NPBRS) to identify multiple skills in the set of demonstrations. NPBRS uses maximum entropy IRL to estimate a set of unknown reward functions that maximizes the likelihood of the demonstrations.
Boularias et al. (2012) propose structured apprenticeship learning. This technique builds on the concept of maximum entropy IRL, but assumes a probability distribution over policies as opposed to over trajectories. The objective in structured apprenticeship learning is to find the distribution over policies that maximizes entropy and closely matches the feature expectation. The reward weights are learned during the maximization process.
Miscellaneous IRL methods
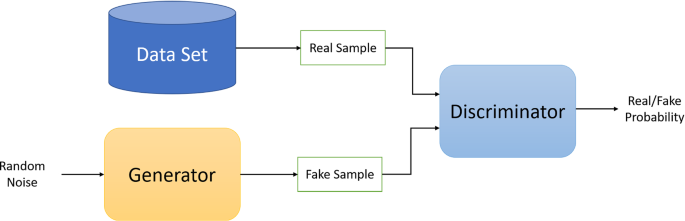
Basic structure of generative adversarial network
Generative adversarial networks (GANs) pair two neural networks, where a generator creates new data with the objective of confusing the discriminator, and the discriminator attempts to determine if an observation is a sample from the data set or a fake sample created by the generator (Goodfellow et al. 2014). Figure 4 displays the basic structure of a GAN. This concept has been extended to IRL. Generative adversarial imitation learning (GAIL) (Ho and Ermon 2016) extends the concepts proposed by Ho et al. (2016) but uses a GAN to learn the expert's policy. Hausman et al. (2017) build on GAIL and propose a framework that can accommodate unlabeled and unstructured data, i.e., data consisting of multiple tasks without corresponding labels distinguishing the tasks. OptionGAN (Henderson et al. 2018) further generalizes to the scenario where the demonstrations are produced by multiple reward functions.
Hahn and Zoubir (2015) frame the IRL problem as a generative probabilistic model. This work is based upon prior work (Toussaint and Storkey 2006) in RL that also formulates the problem as a generative probabilistic model. Toussaint and Storkey (2006) propose modeling the reward as a mixture with K components, where K is the length of the trajectory. This model assumes that the reward is only received at the end of each mixture component. This joint distribution is
$$\begin{aligned} {\mathbb {P}}(r,s_{1:k},a_{1:k}|k) = {\mathbb {P}}(s_1){\mathbb {P}}(a_1|s_1) \prod _{n=2}^k {\mathbb {P}}(s_n|s_{n-1},a_n) {\mathbb {P}}(a_n|s_n) {\mathbb {P}}(r|s_k,a_k). \end{aligned}$$
(28)
Under this model, the probability of the reward is equivalent to the reward function, and the marginal distribution is \({\mathbb {P}}(r,s_{1:K},a_{1:K}) = \sum _{k=1}^K {\mathbb {P}}(r,s_{1:k},a_{1:k}|k) {\mathbb {P}}(k)\). Toussaint and Storkey demonstrate that this marginal distribution can be calculated recursively for the forward RL problem. Hahn and Zoubir leverage this to derive an EM algorithm for the IRL problem.
The reward function is assumed to be a linear combination of basis functions \(R(s,a) = \sum _{d=1}^D \alpha _d \phi _d\). The reward is also assumed to follow a Gaussian distribution \({\mathbb {P}}(r|s,a) = {\mathcal {N}}(r|R(s,a),\sigma _r^2)\). The complete data likelihood for M independent trajectories is
$$\begin{aligned} \begin{aligned} {\mathbb {P}}_\theta ({\mathcal {T}},r,k)&= \prod _{m=1}^M {\mathbb {P}}_\theta (r,s_{1:k}^{(m)},a_{1:k}^{(m)}|k) {\mathbb {P}}(k)\\&= \prod _{m=1}^M \left( \prod _{n=1}^k {\mathbb {P}}_\theta (a_n^{(m)}|s_n^{(m)}) \right) {\mathbb {P}}_\theta (r|s_n^{(m)},a_n^{(m)}), \end{aligned} \end{aligned}$$
(29)
where \(\theta\) is the set of parameters that includes the reward weights and the parameters for the policy, and \({\mathbb {P}}_\theta (\cdot |\cdot )\) indicates that the distribution is dependent on \(\theta\). The Q function for the EM algorithm is
$$\begin{aligned} \begin{aligned} Q(\theta |\theta ') =&\int \sum _{k=1}^\infty {\mathbb {P}}_{\theta ^\prime }(k,r|{\mathcal {T}}) \Bigg ( \sum _{m=1}^M \Big ( \log {\mathbb {P}}_\theta (r|s_k^{(m)},a_k^{(m)}) \\&+ \sum _{n=1}^k \log {\mathbb {P}}_\theta \left( a_n^{(m)}|s_n^{(m)}\right) \Big ) \Bigg ) dr + C, \end{aligned} \end{aligned}$$
(30)
where \(\theta '\) is the set of parameters from the previous iteration, and C represent the constant terms. The E and M steps of the EM algorithm can be derived from the Q function.
Doerr et al. (2015) propose an algorithm that poses the IRL problem as an RL problem. An RL agent is tasked with finding reward weights using the policy search algorithm where the corresponding optimal policy produces trajectories similar to the expert's trajectories. Adversarial IOC (Chen et al. 2016) considers the situation where the demonstrator and the learning agent operate under different sequential decision models. For example, the demonstrator and the learning agent have different capabilities which leads to a difference in the action space, or they operate in different environments which leads to a difference in the transition dynamics. Adversarial IOC is posed as a zero-sum game where the learning agent is trying to learn a control policy that minimizes a loss function, and an adversarial agent is trying to learn a control policy that mimics the demonstrations but also maximizes the learning agent's loss.
Babes et al. (2011) develop an apprenticeship learning algorithm that assumes that multiple agents with different reward functions provide the set of expert trajectories. They propose using the EM algorithm to cluster the trajectories and then use IRL or apprenticeship learning to estimate either the expert's reward or policy, respectively. Nguyen et al. (201) use the EM algorithm to estimate locally consistent rewards. Their IRL formulation is similar to that in Choi and Kim (2012) where it is assumed that the agent is optimizing multiple reward functions.
Many IRL methods require reward features or basis functions, which must be selected a priori. Levine et al. (2010) present a method that simultaneously constructs reward features and estimates the reward weights. The objective is to reduce the reward feature space from a set of possible features to a set of relevant features. This method iteratively adds features to the reward feature set \(\Phi\). Each iteration is composed of two steps. The first step finds the reward function that best fits the current feature set \(\Phi ^k\) and the provided demonstrations. The second step generates a new feature set \(\Phi ^{k+1}\) that improves on the reward function variation. Klein et al. (2011) demonstrate that a set of \(|{\mathcal {S}}|-2\) features exist in the reward space that are relevant to the IRL problem.
Most IRL formulations assume that the expert is risk neutral, i.e., the expert is attempting to maximize the expectation of future reward. However, some expert's or systems may not be risk neutral and may, for example, attempt to maximize the minimum possible future reward. To address this situation, Majumdar et al. (2017) propose risk-sensitive IRL. A risk metric maps an uncertain reward to a real number. Majumdar et al. outline procedures for estimating the risk metric when the reward function is known and the more general case where both are unknown. This work is extended in Singh et al. (2018), which includes improvements to the model and the algorithm and expanded validation experiments.
Behavior cloning, a form of imitation learning and apprenticeship learning, often uses a supervised classifier to learn a mapping of states to actions that replicate the behavior of the provided trajectories. Ratliff et al. (2009) propose inverse optimal heuristic control which combines a behavior cloning classifier with a traditional IRL paradigm. Gradient optimization is used to estimate the weights of the reward function.
Linearly-solvable MDPs (Kappen 2005; Todorov 2007) are a special case of the general MDP where the action is interpreted as a stochastic state selection process. In other words, the agent controls the dynamics of the system rather than taking an action by selecting a state to which they wish to move. A policy for linearly-solvable MDPs is generally written as \(\pi (s^\prime |s)\). Dvijotham and Todorov (2010) develop a maximum likelihood estimation IRL algorithm for linearly-solvable MDPs.
Extensions of IRL
This section outlines areas in the IRL literature that have been studied but need further development in order to make IRL commonly used in real-world systems. The first extension to IRL is model-free methods. While the model-based methods outlined in the previous section represent a significant advance in the field, the reliance on a model limits the real-world application of IRL. The second extension to IRL involves active learning and feedback. In the basic IRL paradigm, the demonstrations are provided to the IRL algorithm. This extension allows for feedback to be requested from the expert in order to improve the efficiency of estimating the reward. The final extension is multi-agent IRL. The methods are listed in Table 2.
Model-free IRL
Most IRL methods assume that a model (more specifically the transition function) is known to the learner and that it can be used to solve the forward RL problem in order to evaluate the quality of the estimated reward function. However, in many scenarios, the transition function may be unknown and difficult or impossible to estimate. Some IRL methods only require access to a routine for finding the optimal policy, which could be a model-free RL approach. However, many of these methods need a large number of interactions with the environment in order to converge to an estimate of the optimal policy, which would significantly increase the computation time of the IRL algorithm. In this section, model-free IRL approaches are outlined.
Boularias et al. (2011) propose relative entropy IRL as the first model-free IRL method, which builds on the maximum entropy IRL algorithm (Ziebart et al. 2008). The proposed algorithm minimizes the relative entropy (or KL-divergence) between the empirical distribution of the demonstrations under a baseline policy and the distribution of the demonstrations under the learned policy. Let \(p({\mathcal {T}}_m)\) be the probability distribution of an observed trajectory in the set of trajectories \({\mathcal {T}}\), and let \(q({\mathcal {T}}_m)\) be the probability distribution under the baseline policy and the transition function. The IRL problem can be formulated as minimizing the relative entropy between these two distributions with constraints
$$\begin{aligned}&\text {min}_p\sum _{{\mathcal {T}}_m \in {\mathcal {T}}} p({\mathcal {T}}_m) \ln \left[ \frac{p({\mathcal {T}}_m)}{q({\mathcal {T}}_m)} \right] \\&\quad\text {s.t.}\left| \sum _{{\mathcal {T}}_m \in {\mathcal {T}}} p({\mathcal {T}}_m) f_d^\tau - {\hat{f}}_d \right| \le \epsilon _d \quad d = 1,...,D \\&\qquad\qquad\sum _{{\mathcal {T}}_m \in {\mathcal {T}}} p({\mathcal {T}}_m) = 1 \\&\qquad\qquad p({\mathcal {T}}_m) \ge 0 \quad \forall {\mathcal {T}}_m \in {\mathcal {T}}, \end{aligned}$$
(31)
where \(f_d^\tau\) is the expected feature count under the learned policy for the \(d^{th}\) feature, and \({\hat{f}}_d\) is the empirical feature count from the observed trajectories. The reward weights \(\alpha\) can be included in the first constraint. The Lagrangian and KKT conditions are used to define the dual problem, and the IRL problem now becomes maximizing the dual with respect to \(\alpha\). Suay et al. (2016) propose using relative entropy IRL to recover dense reward functions that are later used to solve the forward RL problem in a sparse reward environment.
Tossou and Dimitrakakis (2013) develop two model-free IRL algorithms, which are extensions of model-based Bayesian approaches (Dimitrakakis and Rothkopf 2011; Rothkopf and Dimitrakakis 2011). The first model, called the reward prior model, uses a different parameterization of the reward function and a model-free method for estimating the value function. The second model, called the policy optimality model, uses a prior distribution on the policy and estimates a posterior on the policy from the data. Several variations of these models using different prior distributions are outlined.
Ho et al. (2016) set the model-free IRL problem as an apprenticeship learning problem. The objective of the proposed method is to find an optimal policy that matches the expert's. However, there is a subroutine which estimates the cost function. This method assumes that the true cost function c is within a set of possible cost functions \({\mathcal {C}}\). First, the state visitation distribution is defined as \(\rho _\pi (s) = \sum _{t=0}^\infty \gamma ^t {\mathbb {P}}_{p_0,\pi }(s_t=s)\). \({\mathbb {P}}_{p_0,\pi }(s_t=s)\) is the probability of being in s at t when the initial state is sampled from \(p_0\) and then \(\pi\) is followed. The state-action visitation distribution is \(\rho _\pi (s,a) = \pi (a|s) \rho _\pi (s)\). The expected cost can be calculated using \(\eta ^c(\pi ) = \sum _{s,a} \rho _\pi (s,a) c(s,a)\). The objective function for the proposed apprenticeship learning algorithm is \(\text {min}_\pi \; \text {sup}_{c \in c} \eta ^c(\pi ) - \eta ^c(\pi _E)\).
Klein et al. (2012) suggest using structured classification as a model-free IRL method. The proposed idea learns a multi-class classifier that mimics the expert's policy. An estimate of the expert's feature expectation is used to learn the parameters of a linear scoring function. A classifier is trained that maps the reward basis functions to the reward considering the linear scoring function. The parameters of the learned classifier are the reward weights. A model-free algorithm can be used to estimate the expert's feature expectation, thus making the structured classification IRL method model-free. Klein et al. (2013) later build upon this method and utilize a regression algorithm to estimate the reward function.
Uchibe and Doya (2014) propose a model-free IRL approach that utilizes dynamic policy programming (Azar et al. 2012). In the proposed approach, the reward function is referred to as a cost function l(s,a) and the objective for the forward problem is to find a policy that minimizes expected future cost. Further, the cost function is constrained and has the following form
$$\begin{aligned} l(s,a) = q(s) + \frac{1}{\beta } \text {KL}(\pi (\cdot |s)||\pi _0(\cdot |s)), \end{aligned}$$
(32)
where \(\text {KL}(\pi (\cdot |s)||\pi _0(\cdot |s))\) represents the KL-divergence between two policies, q(s) is the state-dependent cost component, and \(\beta\) is the inverse temperature parameter. The optimal value function can now be written as
$$\begin{aligned} V^*(s) = \text {min}_{\pi (\cdot |s)} \sum _{a \in {\mathcal {A}}} \pi (a|s) \left[ q(s) + \frac{1}{\beta } \ln \left[ \frac{ \pi (a|s)}{\pi _0(a|s)} \right] + \gamma \sum _{s' \in {\mathcal {S}}} P_{s,s'}^a V^*(s') \right] . \end{aligned}$$
(33)
If \(q_{\beta }(s) = \beta q(s)\) and \(V_\beta ^*(s) = \beta V^*(s)\), then the log ratio of the policies is
$$\begin{aligned} \ln \left[ \frac{ \pi (a|s)}{\pi _0(a|s)} \right] = q_\beta (s) + \gamma \sum _{s' \in {\mathcal {S}}} P_{s,s'}^a V_\beta ^*(s') - V_\beta ^*(s). \end{aligned}$$
(34)
The IRL problem is now broken into two parts. The first estimates the log ratio of the stochastic policies, and the second estimates the cost and value functions. Assume that two demonstration sets are provided, where \({\mathcal {T}}^\pi\) is produced under policy \(\pi\), and \({\mathcal {T}}^0\) is produced under policy \(\pi _0\). Least squares conditional density estimation (Sugiyama et al. 2010) is used to estimate the negative ratio of these policies. Least squares with regularization is used to estimate the linearly parameterized cost \({\hat{q}}_\beta (s;{\varvec{w}}_q^\intercal ) = {\varvec{w}}_q^\intercal \psi _q(s)\) and value functions \({\hat{V}}_\beta ^*(s;{\varvec{w}}_V^\intercal ) = {\varvec{w}}_V^\intercal \psi _V(s)\), where \({\varvec{w}}\) are the parameters and \(\psi\) are the basis functions. Theoretically, any basis function could be selected but Gaussian functions are recommended by Ucbibe and Doya. Uchibe later extends this work and utilizes deep learning architectures to estimate the cost and value functions instead of the least squares method (Uchibe 2016; Uchibe 2018).
Herman et al. (2016) propose maximizing the likelihood with respect to the reward function and the system dynamics simultaneously by learning both components of the MDP. Herman et al. suggest that it may be advantageous to learn the true transition function and the agent's belief about the transition function, designated \({\mathbb {P}}_A(s'|s,a)\), as these two functions may be different. Therefore, the proposed algorithm estimates three sets of parameters
-
\(\varvec{\theta }_R\) - The reward feature weights,
-
\(\varvec{\theta }_{T_A}\) - The parameters of the agent's transition function,
-
\(\varvec{\theta }_T\) - The parameters of the true transition function.
The likelihood of the demonstrated trajectories is
$$\begin{aligned} {\mathbb {P}}\left( {\mathcal {T}}|\varvec{\theta }\right) = \prod _{{\mathcal {T}}_m \in {\mathcal {T}}} {\mathbb {P}}\left( s_1^{{\mathcal {T}}_m}\right) \prod _{t=1}^{T_m-1} \left[ \pi _{\varvec{\theta }} \left( s_t^{{\mathcal {T}}_m}|a_t^{{\mathcal {T}}_m}\right) {\mathbb {P}}_{\varvec{\theta }_T}\left( s_{t+1}^{{\mathcal {T}}_m}|s_t^{{\mathcal {T}}_m},a_t^{{\mathcal {T}}_m}\right) \right] , \end{aligned}$$
(35)
where \(\varvec{\theta } = [ \varvec{\theta }_R \; \varvec{\theta }_{T_A} \; \varvec{\theta }_T]\). Note that the the transition function is only dependent on \(\varvec{\theta }_T\), while the policy is dependent upon \(\varvec{\theta }_R\) and \(\varvec{\theta }_{T_A}\). The gradient of the log likelihood is used to update the parameters. Herman et al. (2016) expand this work to the situation where the agent's stochastic policy mapping is also unknown and needs to be estimated.
Kangasrääsiö and Kaski (2018) present a model-free IRL method where only partial expert trajectories are available. The authors present three methods to estimate the rewards under this assumption. The first computes the exact likelihood. The second utilizes Monte-Carlo estimation of the likelihood. The third uses an approximate Bayesian computation approach (Sunnåker et al. 2013) to evaluate the likelihood. Makino and Takeuchi (2012) propose two methods for learning the components of a POMDP which include the transition function and the reward function. The first uses the COBYLA algorithm (Powell 1998) to find local MAP estimates for the parameters, and the second uses an MCMC sampler.
Active learning and feedback
In general, active learning is an area of machine learning where the learning agent can query an unlabeled data set and ask that an expert label specific examples (Settles 2012). By selecting specific examples, the learning agent hopes to learn with fewer labeled examples. The basic active learning framework is displayed in Fig. 5. This section outlines IRL algorithms that utilize active learning concepts and interact with the expert who is providing feedback.
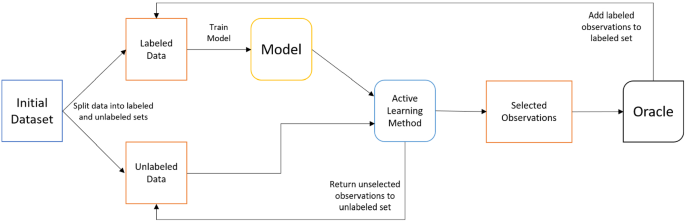
Basic active learning framework
Lopes et al. (2009) utilize the Bayesian IRL framework and active learning concepts to reduce the number of demonstrations needed to estimate the reward function. In this framework, the learner is able to query the expert with regard to their action. The learner selects the queried state based on the current posterior estimate of the reward function. Sadigh et al. (2017) also propose an active learning technique for IRL, but their work assumes that a human provides a preference between two sample trajectories. Kunapuli et al. (2013) utilize preference elicitation to incorporate information from the human expert about their preference for actions in a specific state. Ezzeddine et al. (2018) use feedback from a human trainer when the provided demonstrations are sub-optimal. The human trainer provides feedback in the form of positive and negative reinforcement with respect to the action in the demonstration set.
El Asri et al. (2016) propose score-based IRL (SBIRL) where each trajectory is provided a score from an outside expert who may not produce accurate scores. The scores are interpreted as noisy estimates of the sum of discounted future rewards. One advantage of SBIRL is that the collected trajectories can be produced by an optimal or sub-optimal policy. Reward weights are estimated by solving a linear least-squares problem
$$\begin{aligned} \begin{aligned} \alpha _m&= \text {argmin}_{\alpha _m} \frac{1}{M} \sum _{m=1}^M (v_m - \alpha ^\intercal \mu ({\mathcal {T}}_m))^2 \\&= \left( \frac{1}{M} \sum _{m=1}^M \mu ({\mathcal {T}}_m) \mu ({\mathcal {T}}_m)^\intercal \right) ^{-1} \frac{1}{M} \sum _{m=1}^M \mu ({\mathcal {T}}_m) v_m, \end{aligned} \end{aligned}$$
(36)
where \(v_m\) is the score for the \(m^{th}\) trajectory, and \(\mu\) is the empirical discounted sum of the reward features.
Odom and Natarajan (2016) propose active advice seeking IRL, which is a more expressive form of interaction with a human operator and has two advantages over active learning: it can receive information over a large portion of the feature space, and it can receive a set of optimal labels as opposed to a single label. The set of provided labels convey information about actions that are preferred and actions that should be avoided. Pan and Shen (2018) propose human-interactive IRL. In this method, the human first supplies full demonstrations and also defines subgoals for the agent. The agent then learns from the provided demonstrations and attempts to complete the tasks. The human can then provide further feedback in the form of additional full demonstrations or specific feedback on the subgoals.
In order to incorporate a notion of safety when a robot is interacting with a human, Amin et al. (2017) propose repeated IRL. The human provides feedback to the robotic agent whenever the human is "surprised" by the agent's policy. The agent's objective is to find a policy that minimizes the number of times the human is surprised. Woodworth et al. (2018) relax some of the assumptions made by repeated IRL and propose observational repeated IRL. This algorithm does not assume that the human can provide feedback to the agent.
Multi-agent IRL
Most IRL algorithms address the problem of a single agent interacting with an environment. This section outlines multi-agent IRL (MIRL) where multiple agents are interacting with the environment and each other. One possible solution is to model each agent independently and assume that the actions of the other agents are part of the stochastic nature of the environment. However, this may produce suboptimal results in situations where the agents are coordinating their actions to maximize a joint reward function.
Natarajan et al. (2010) were the first to tackle the MIRL problem. Their goal is to learn the reward functions of multiple agents acting independently in an environment and then estimate a policy for all agents for a central controller. Natarajan et al. assume an average-reward MDP. The Bellman equation for this type of MDP is
$$\begin{aligned} V^\pi (s) = r_s(\pi (s)) + \sum _{s' \in {\mathcal {S}}} P_{s,s'}^{\pi (s)} V^\pi (s) - \rho , \end{aligned}$$
(37)
where \(\rho\) is the average reward under \(\pi\). H-learning (Tadepalli and Ok 1998) can be used to solve the forward RL problem for an average-reward MDP. In line with the work of Ng and Russell (2000), Natarajan et al. derive the following constraint
$$\begin{aligned} ({\varvec{P}}_{a_1} - {\varvec{P}}_a) ({\varvec{I}}-{\varvec{P}}_{a_1})^{-1} (\mathbf{R} - \varvec{\rho }) \ge 0 \quad \forall a \in {\mathcal {A}}\backslash a_1. \end{aligned}$$
(38)
In the case of multiple agents, the average adjusted reward vector \((\mathbf{R} - \varvec{\rho })\) can be replaced with \(\sum _{i=1}^I w_i (\mathbf{R} _i - \varvec{\rho }_i) = \Theta \mathbf{w}\), where I is the number of agents, \(\Theta = \{\varvec{\theta }_1,...,\varvec{\theta }_I\}\), and \(\varvec{\theta }_i\) is the average adjusted reward for agent i. Using the updated constraint, rewards are estimated using the following optimization problem
$$\begin{aligned} \begin{aligned} \underset{\varvec{\theta }_1,...,\varvec{\theta }_T}{\text {max}}&-\lambda || \varvec{\theta }|| + \sum _{m=1}^M \underset{a \in {\mathcal {A}} \backslash a_1}{\text {min}} ({\varvec{P}}_{a_1}(m) - {\varvec{P}}_a(m)) ({\varvec{I}} - {\varvec{P}}_{a_1})^{-1} \varvec{\theta } \\ \text {s.t.}&\quad ({\varvec{P}}_{a_1} - {\varvec{P}}_a) ({\varvec{I}} - {\varvec{P}}_{a_1})^{-1} \varvec{\theta } \succeq 0 \quad \forall a \in {\mathcal {A}}\setminus a_1 \\&\quad \varvec{\theta } = \sum _{i=1}^I \varvec{\theta }_i w_i \\&\quad |\theta _i^j| < \theta _{max}, \quad \text {for} \; i=1,...,I, \;\text {and}\; m=1,...,M. \end{aligned} \end{aligned}$$
(39)
Reddy et al. (2012) also expand the original IRL formulation in Ng and Russell (2000) to the multi-agent setting. Their work focuses on non-cooperative agents and general sum stochastic games. The Nash equilibrium (Nash 1950) is a fundamental concept in game theory, and Reddy et al. present a theorem that rewrites the Nash equilibrium in the multi-agent RL framework. Using this result, the optimal reward function must satisfy the following condition: \(Q(s,\pi _i \pi _{-i}(s)) \ge Q(s,a_i \pi _{-i}(s)), \; \forall a_i \in {\mathcal {A}}_i\), where \(\pi _i\) is the strategy for agent i in response to the strategy profile \(\pi _{-i}\), i.e. the strategies of all agents except i. Using this condition, the constraint from Ng and Russell (2000) can be rewritten as
$$\begin{aligned} \left( {\varvec{P}}_{\pi _i^*,\pi _{-i}^*} - {\varvec{P}}_{a_i,\pi _{-i}^*}\right) \left( {\varvec{I}}- \gamma {\varvec{P}}_{\pi _i^*,\pi _{-i}^*}\right) ^{-1} \mathbf{R} _i \ge 0. \end{aligned}$$
(40)
Reddy et al. present algorithms for estimating the reward function when the policy is known and for when the policy is unknown but sample trajectories are provided.
Bogert and Doshi (2014) investigate the situation where multiple robots are interacting in an environment but trajectory information from other robots can be occluded. This multi-agent IRL approach builds on the maximum entropy IRL algorithm presented in Ziebart et al. (2008). In order to reduce the size of the joint state and action spaces, each robot is modeled using a separate MDP except when the robots must interact. When the robots must interact, their actions are modeled as a Nash equilibrium for a game. Bogert and Doshi (2015) extend this work to the model-free setting where they develop an algorithm that simultaneously estimates rewards and transition probabilities.
Lin et al. (2018) take a Bayesian approach to MIRL and build upon the work by Qiao and Beling (2011). The presented method is specific to two-player zero-sum games. In this type of game, the reward function is symmetric \(r^1(s,a^1,a^2) = -r^2(s,a^1,a^2)\), where the superscripts designate the player. An optimization problem with constraints is formulated that is similar to the MAP estimation proposed by Qiao and Beling (2011) and assumes a Gaussian prior on the rewards. This approach is later built upon and expanded to general sum games (Lin et al. 2019). Zhang et al. (2019) develop non-cooperative IRL in the context of zero-sum games where the agents' reward functions are in conflict and only one agent knows the true reward, i.e., the joint reward function of both agents.
In certain situations, there could be a mixture of the type of agent in the system, for example, robotic agents and human agents. Hadfield-Menell et al. (2016) investigate the situation where a robotic agent and a human agent are cooperatively working to maximize the human's reward function. Hadfield-Menell et al. argue against the classic single-agent formulation for this setting for two reasons. First, the robot should not directly learn the humans reward function because this could generate unnecessary behavior. Second, the classic formulation does not allow for the human to provide teaching demonstrations, i.e., demonstrations that are sub-optimal for the task but can provide vital information for teaching the robot. In order to address this problem, Hadfield-Manell et al. propose cooperative IRL (CIRL) and formulate it as a two-player game with partial information for the robot. The human player knows the reward function being maximized, but the robot must learn the reward function by playing the game. In the end, Hadfield-Manell et al. demonstrate that this problem can be reduced to a single-agent POMDP.
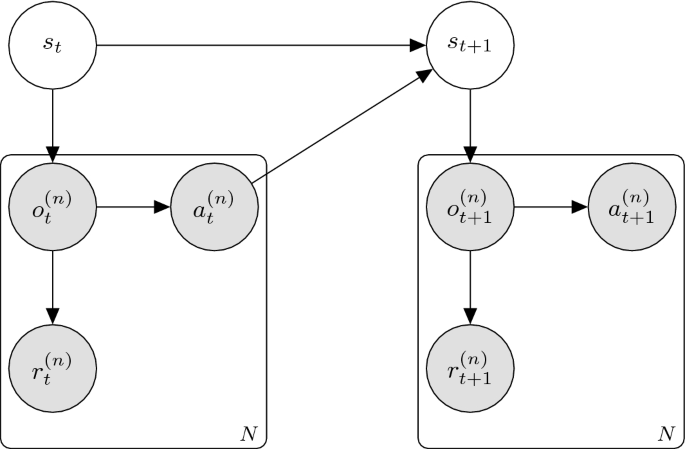
Graphical model of a swarMDP (Šošic et al. 2017). N is the number of agents in the system
Šošic et al. (2017) study homogeneous or swarm systems and attempt to find a single local reward function that explains the global behavior of the system. In homogeneous systems, agents are assumed to have a similar architecture and are interchangeable. Agents are also assumed to be restricted to local areas of the system, meaning they only receive information that is within a predetermined region. A swarMDP (Fig. 6) is formulated for this type of system, and it is demonstrated that MIRL for this type of system can be reduced to the single-agent case.
Source: https://link.springer.com/article/10.1007/s10462-021-10108-x
0 Response to "Max Margin Planning for Continuous Domain"
ارسال یک نظر